資料ダウンロードBOXリンク:https://tdu.box.com/s/cjmy1v42ksmf5d2l1c50s9jqoq0gkbja
[研究背景]
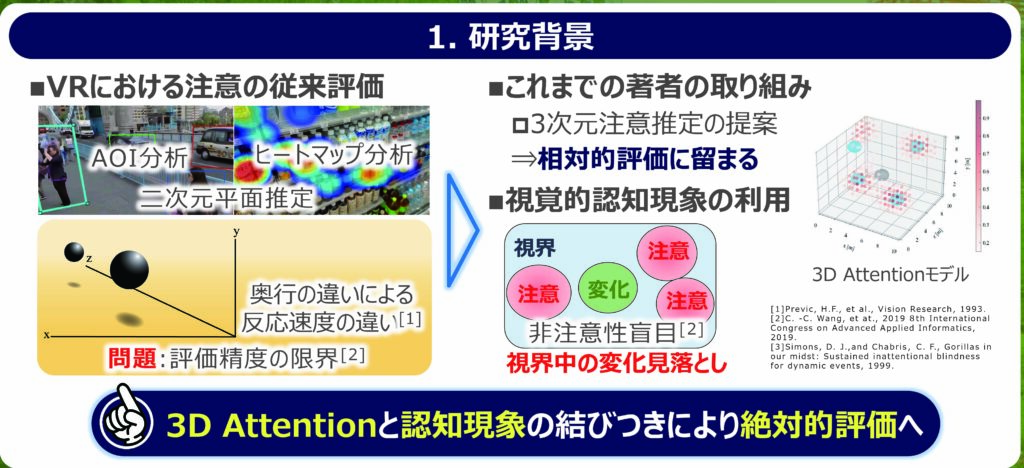
これまで,VR(仮想環境)における視覚的注意の評価は,二次元平面推定が利用されてきた.しかし,これらの評価指標には奥行に関する評価に対して精度の限界が指摘されている.この問題の解決のため,著者は三次元で視覚的注意を推定できる数理モデル「3D Attention」を提案し,検証を続けてきた.本研究では,相対評価に留まっていた3D Attentionを視覚的認知現象との関係を明らかにし,絶対評価として活用可能となることを目指す.この視覚的認知現象には,「非注意性盲目(Inattentional Blindness)」という現象に着目した.非注意性盲目とは,ユーザーの注意が他の対象に集中しているために,視界内で起こる顕著な変化や重要な情報を見落としてしまう現象である.
[目的]
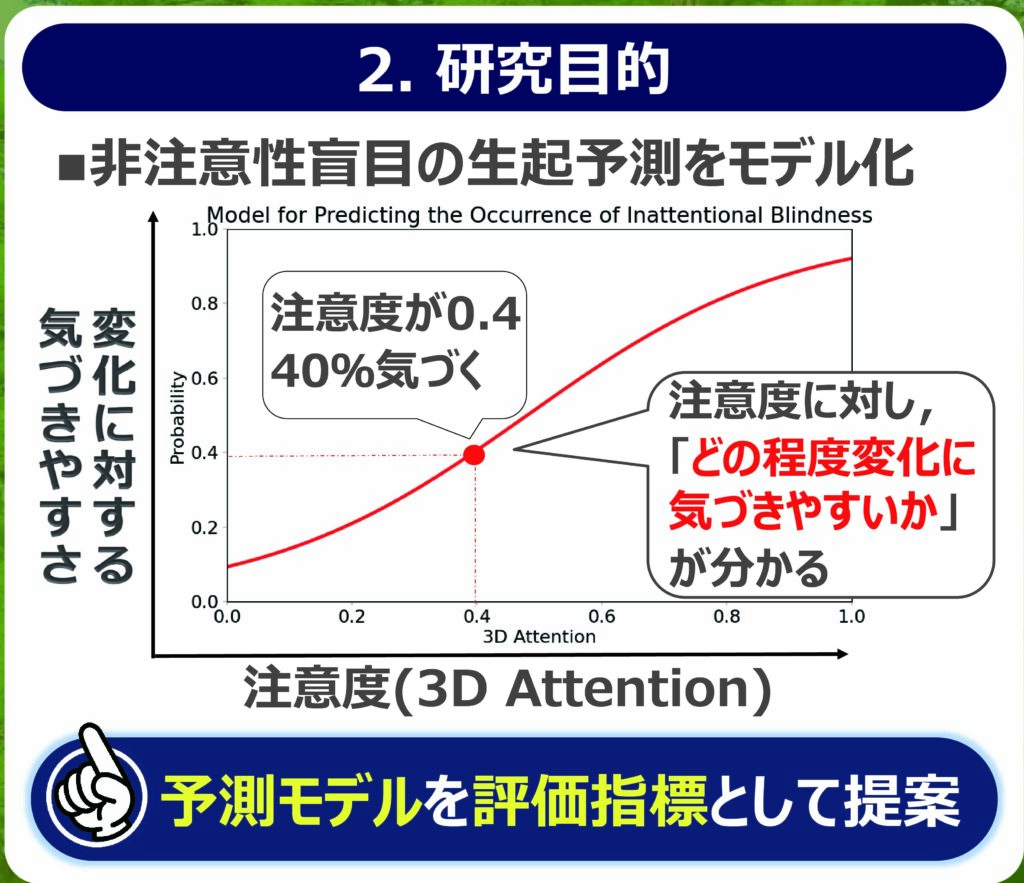
本研究の成功により,VRユーザーの視線データを用いて,任意の環境と箇所で非注意性盲目が発生しやすいかを特定できるようになる.これは,VRユーザーの視覚的注意における客観的評価指標となる.そして,これはVRアプリケーションのデザイン改善に直接役立つだけでなく,例えば自動車の運転支援システムを例とした他の分野への応用も可能となる.このように,本研究はVR技術の新たな可能性を探ると共に,人間の認知過程に関する深い理解を促進することを目指す.
[提案手法(説明変数の生成)]
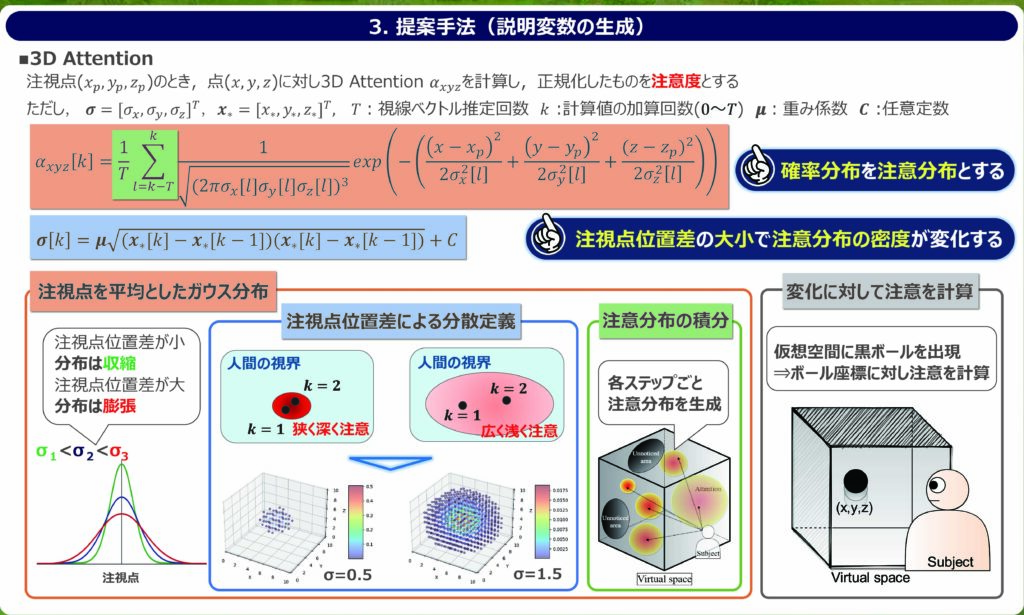
本稿では,以前提案した人の視覚的注意を推定可能な3D Attentionをモデル化に用いる.3D Attention は,注視点座標から視覚的注意を計算し出力する数理モデルであり,計算結果をユーザーごと正規化し注意度と定義する.
そして,3D Attention は注視点(x_p,y_p,z_p)とした時のある点(x,y,z)の3D Attention α_xyzとして定義する.ただし,σ=[σ_x,σ_y,σ_z]^T, x_*=[x,y,z]^Tである.
この関数は,ガウス分布を基に考案され,空間上に設けた(x,y,z)に計算された数値を保存する.3D Attention の計算値は人間がどの程度注意をしているかを表す指標となり,積分によって(x,y,z)に加算される.
ここで,T は注視点の算出回数,k は0 ~ Tの値を取る計算値の加算回数,μは,実験や測定環境によって自由に設定できる重み係数である.この重み係数はexp関数の広がりを決定づける.つまり視覚的注意のひろがりを決めるものである.
また,パラメータであるσは注視点の変化量,即ち視線速度により変化する.これは注視点位置差が大きいときは広い範囲を浅く注意し,注視点位置差が小さいときは狭い範囲を深く注意している状態を再現する.加えて,Cの値は視線速度がゼロの場合,最も注意している範囲を表す.
[提案手法(モデル化)]
本研究では,非注意性盲目の予測にロジスティック回帰モデルを採用した.採用理由として,非注意性盲目の発生確率を直接的に出力できる利点が挙げられる.このモデルは3D Attentionを使用して,注視点の座標から注意度を算出し,注意度を説明変数として設定した.この説明変数には,非注意性盲目が生じた箇所の注意度を用いた.また,目的変数として,非注意性盲目の発生結果を1(非発生)または0(発生)で表した.
さらに,前述したヒトの注意分布の強度と範囲を決定するT,μ,Cについては,モデルの予測正解率が最大化するようにパラメータチューニングを行った.このパラメータチューニングには,ベイズ最適化を採用し,PythonライブラリのOptunaを使用した.

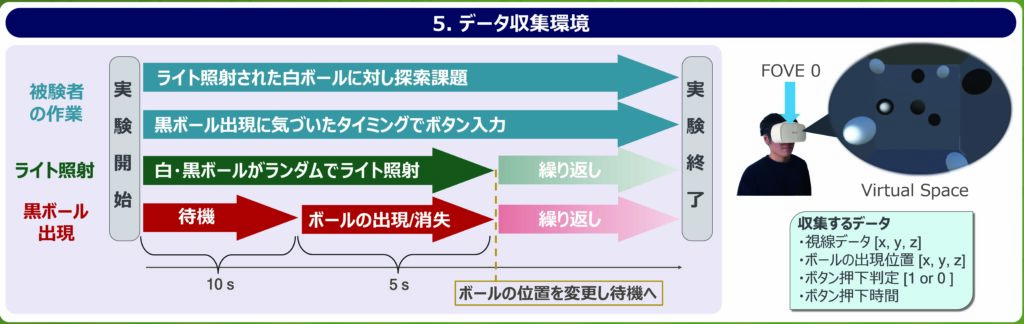
[データ収集環境]
以下のタイムチャートは,実験の流れについて説明したものである.VR 空間はVR 型のアイトラッキングデバイスであるFOVE 0 によって提示を行った.FOVE 0は120 Hzのフレームレートでアイトラッキングデータが取得可能である.
VR 空間は10×10×10 mの部屋となっており,内部には白と黒のボールを配置した.配置された白と黒のボールは,ランダムで1つ選びライトで照射を行った.黒のボールにおける出現と消失の挙動は,被験者に非注意性盲目を生起させるために設けた.10 秒間の待機状態が行われたのち,5 秒かけて出現と消失を行う.この合わせて15 秒間のサイクルは計10回行い,一度の実験で10 個のデータ収集を行った.
また,被験者の課題は2 種類設けた.1 つ目の課題はライトで照射する白のボールを目で追う視覚探索課題を設けた.このような視覚探索課題は,先行研究により注意性盲目を生起させやすくすることが報告されている.2 つ目の課題は,出現と消失を行う黒のボールに気づいた場合,ボタン入力する課題を設けた.このボタン入力結果は非注意性盲目の生起結果とし,気づいた場合は1 を気づかなかった場合は0 で記録した.
以上よりこの実験において,実験中のユーザーの注視点座標データ(x,y,z),ボールの出現座標(x,y,z),ボタンの押下結果(1 or 0)を記録した.
[結果]
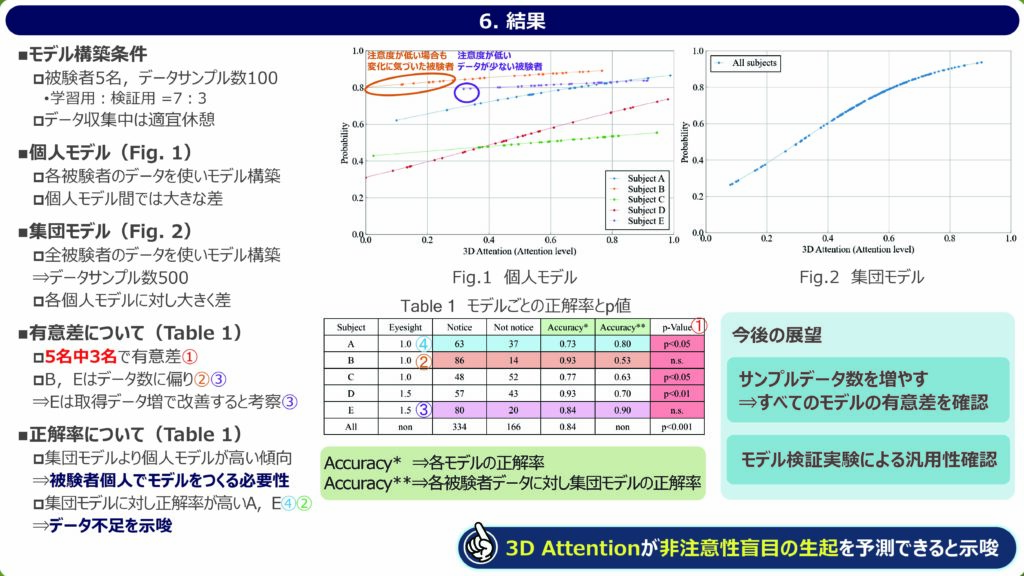
{モデルの有意差について}
被験者5 名のうち3 名のモデルに有意差が確認された.また被験者5 名全員のデータを利用し構築したモデルにおいても有意差を示した.これは,本稿の目的である非注意性盲目における生起予測モデルの構築が成功したと示唆する.
また,正解率とp値の関係についての相関が見られないことが分かる.特に被験者のデータに偏りが存在するSubject BとSubject Eで顕著である.これは,黒のボールに気づく回数が多い場合,多くの注意度の入力でモデルは「気づいた」と予測することが起因する.この場合はモデルの正解率は自然と高くなるが,モデルが正確に非注意性盲目を予測しているわけではなく,単にデータの偏りにより発生する.その結果,モデルが実際には区別する力が低いにも関わらず,高い正解率が示される.一方で,非注意性盲目が生じなかった(気づいた)注意度のデータが多数を占める場合,モデルは気づかなかった注意度を正確に予測する機会が少ないため,性能を示すp値は不利な結果となる.つまり,有意差が出なかった2 名の被験者においても取得データ数を増やすことでモデルに有意差が出ると推測する.
{モデルの汎用性について}
Fig. 1を参照すると,各被験者における注意度と非注意性盲目の発生率には明らかな違いが存在することが確認できる.特に,Subject Bは低いから高い注意度にかけて80 %以上の識別率を維持しており,他の被験者よりも黒のボールに気づきやすい傾向にあることが示された.これは,Table 1で見られるように,Subject Bが他の被験者に比べてより多くの回数でボールを認識していることに起因する.一方で,Subject Cは注意度が変化しても約50 %の認識率を維持し,非注意性盲目の発生有無を効果的に判別できていないことが示された.これらの被験者間の差異は,提案されたモデルの汎用性に影響を与える可能性がある.実際のシステムへの組み込みを検討する場合,システムをユーザーそれぞれにカスタマイズされたモデルを作成する必要が生じる.よって,今後の研究では被験者全員のデータで構築したモデルが,実際のユーザーの非注意性盲目の発生率と,どの程度乖離があるのかを検証することが重要である.